The Standard Model of Particle Physics
FEST log
Entry #012
July 10, 2024
Physics, act 3: material reality as quantum fields
Toward the end of entry #009, I introduced 1925 as the year that ended "classical physics", act 1 in the play of physics as the science of matter. That act started with the publication of Newton's Principia in 1687. During the subsequent 238 years, the accepted scientific worldview was that the material cosmos could be viewed as a mechanism. Not only that; any future state of the cosmos could in principle be derived from knowledge of the current state.
The opening of act 2 took place in 1925 with the discovery of quantum mechanics, which triggered a worldview in which matter did not behave at all like clockwork type deterministic mechanics. Instead, on atomic and subatomic scales, the best description was that matter and energy consisted of discrete packages, quanta, which were neither actual nor potential in terms of their properties, but some mysterious mix of both.
It is hard to overstate the shock that physicists experienced in 1925, when they were forced to accept the fact that their best model of material reality was now based on a kind of probabilistic mix of "real" and "possible" in ways not foreseen by anybody. I mentioned in entry #010 that physicists knew, already in 1925, that they had entered a whole new area. What is more, it was an intermediate period, a kind of "Middle Ages" of an unusual type, where the people living in that period had already realized that it was a "middle" age.
I consider 1975 as marking the opening of yet another act of physics. Whereas the opening of act 2 ushered in a new period of bewilderment, 1975 marked the start of a much happier period. The enormous relief that came at the opening of act 3 stemmed from the fact that at last a new form of unification was possible: that of the standard model of particle physics. Almost overnight, a way was found to describe material reality as based on a set of related quantum fields, to be discussed below.
To put this in context, we can add a prescientific act 0, which opened with Aristotle's mechanics around 300 BC, an act that would last 2,000 years. It featured a split unification, one half of which described temporal motion in the Earthly realm, the other half eternal motion in the Heavens above the orbit of the Moon. After act 1, starting with Newton's unification of motion everywhere, and act 2, turning any notion of existence and motion upside down, act 3 resembled that of Aristotle: material reality was unified as governed by quantum fields, while spacetime remained the stage for gravity in its classic field form.
Material reality vs. reality of space and time
In quantum field theory, QFT, each elementary particle has its own field. There is an electron field, and each electron, as well as its antiparticle, the positron, can be viewed as a local excitation of the electron field. The electron field is present everywhere in the Universe. An approximate picture is to view that field as a kind of spacetime-filling ocean, with each electron a localized wave in that ocean. Similarly, each photon is an excitation of the electromagnetic field, also filling the whole Universe in space and time.
The interactions between electrons, as well as other electrically charged particles, and photons are described in QED, quantum electrodynamics. The best reference I know for getting a feel of what this all means, without using any mathematics, is the book "Waves in an impossible sea" by Matt Strassler which I already referenced in entry #010.
After 1975, any elementary particle that we know of, as well its corresponding quantum field, forms part of the unification scheme of the standard model. The only exception is the gravitational field. The classical, pre-quantum description of that field is given by general relativity, GR, and we simply don't know what the quantum equivalent of GR is. One thing we *do* know about the gravitational field is that there is a medium in which the waves that can occur in that field propagate. It is the nothingness of empty spacetime. And when spacetime gets disturbed, its waves carry immaterial energy and momentum.
In contrast, for any of the quantum fields, each one corresponding to a particular elementary particle, we have no idea of what its medium "is". What is more, we don't even know whether it "exists", and what is more, we don't even know whether "existence" is an appropriate term.
If that sounds familiar, it should: we encountered the electromagnetic "aether" already in entry #007, as the proposal by Maxwell to describe what the classical medium could be for his classical theory of electromagnetism. In entry #009 we saw that roughly half a century later Einstein's special relativity ruled out any three-dimensional form of "aether" medium. And in entry #011 the QED formalism gave us the mathematical medium of the QFT of electromagnetism, a new kind of four-dimensional spacetime-based "aether" with no clear physical interpretation except for it being the (non-existent?) carrier for photons.
After this prelude, we are ready to catch the meaning of the title of this section: "Material reality vs. reality of space and time". The first part refers to quantum field theories describing the dynamics of elementary particles. The second part describes gravity, operating in the dynamic medium of spacetime.
Disclaimer: what I have tried to summarize in simple terms is the established view in 2024. Before too long deeper insight might arise that will describe space and time as side effects of a more fundamental theory than general relativity, and in that case the distinction between "material" and "immaterial" may disappear in the next unification. Philosophically speaking, that would be yet another sublation (in the original "Aufhebung") in Hegelian terms.
Mining the history of physics, towards a science of mind
This entry is the fifth and last of our "picture book" series, starting with entry #008, in which I have tried to summarize theory formation in physics, from Galileo to the present. My intent was to map some of the twists and turns, disappointments and surprises, that have characterized the progress of natural science in all of its disciplines. Physics was a convenient place to start, being the oldest discipline, and the first to reach quantitative and accurate reproducible results.
The motivation for me to map fundamental progress in the most basic natural science, was to have at least one concrete example of how a branch of science has grown over time. In entry #006 we started on a trek to search for candidate theories, to go with the two experiments discussed in entry #005. Rather than coming up with ad hoc theories of what a theory of mind studying mind using only mind might look like, the most conservative approach I could think of was to try to find clues from the evolution of theories of matter, using material instruments, aided by the use of mathematics and thought experiments.
The narrative that unfolded in these five entries and the use of these kinds of diagrams are new, to the best of my knowledge. They form an example of what I have witnessed often during my work in interdisciplinary studies. While looking to find a path through the jungle of a whole new terrain, one can fall back on inspecting various beaten paths in more familiar areas. In my experience, one can often discover new clues in the historical processes that led to older paths being constructed.
Down to details
Picture time! After the more than 1400 words used so far in this entry, let's see whether a picture here can be worth more than a thousand words.
The first rays of light and hope after the 1925 shock of the discovery of the mystery of quantum mechanics, were symbolized in entry #011 in Fig. 28, reproduced below. Around 1950 at least one of the known forces, electromagnetism, could be "quantized" to produce QED, quantum electrodynamics, as a relativistic quantum field theory, QFT. But the euphoria upon being able to make amazingly accurate calculations and predictions for electromagnetic interactions between charged particles and photons didn't last long. During the next twenty years, till 1970, neither the strong nor the weak interactions could be treated in the same way as QED, as a QFT.
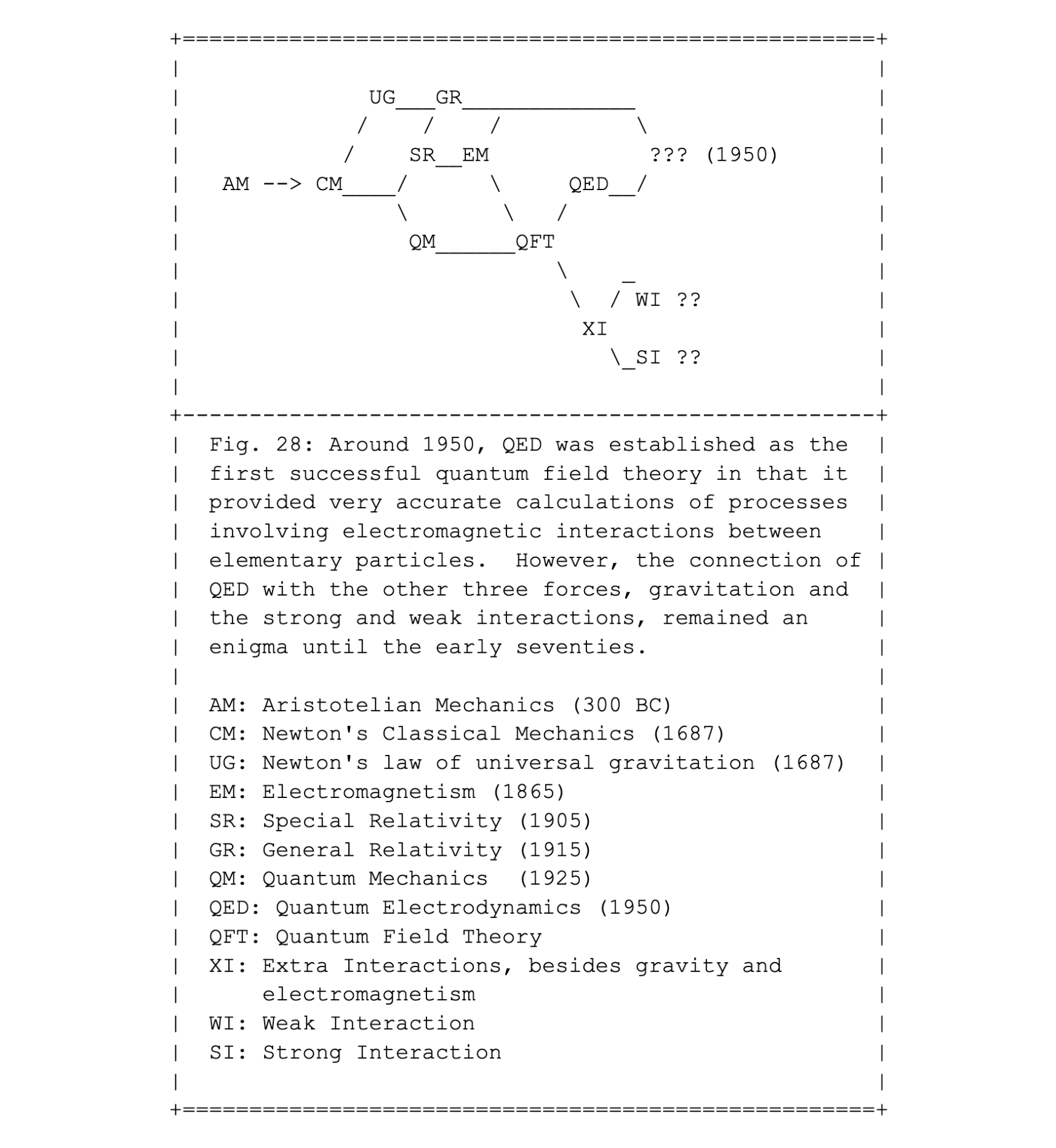
In my attempt to propose a historical division in periods, always a haphazard enterprise, I proposed 1975 as the start of act 3, the discovery of the standard model of particle physics. During a short period spanning only a few years in the early seventies, the standard model was developed and tested as a model that unified all three non-gravitational forces into a single theory. The only field that could not be quantized yet, and therefore not be unified either, was the classical theory of general relativity. This is indicated in Fig. 30 with the three question marks.
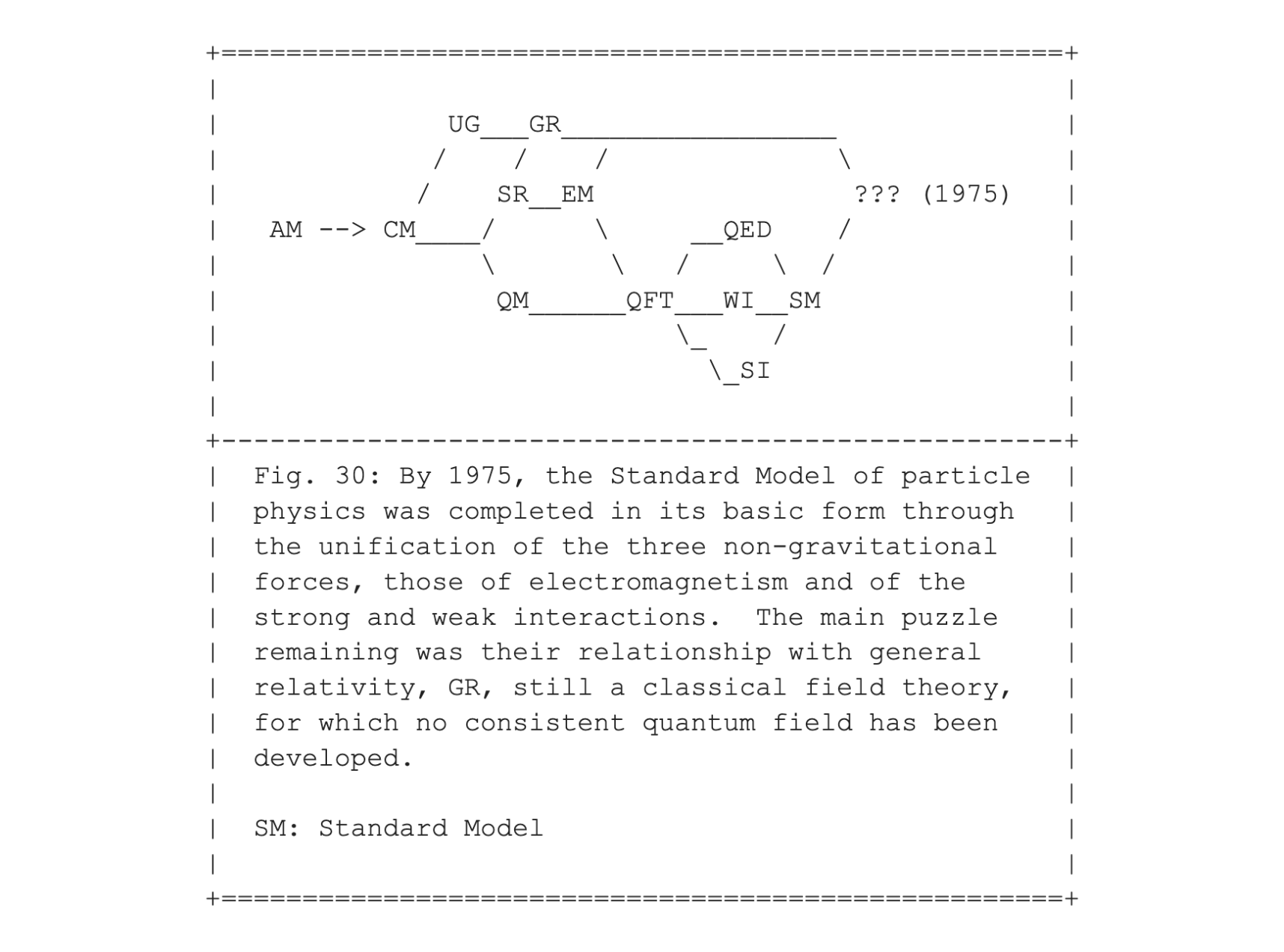
Full Disclosure
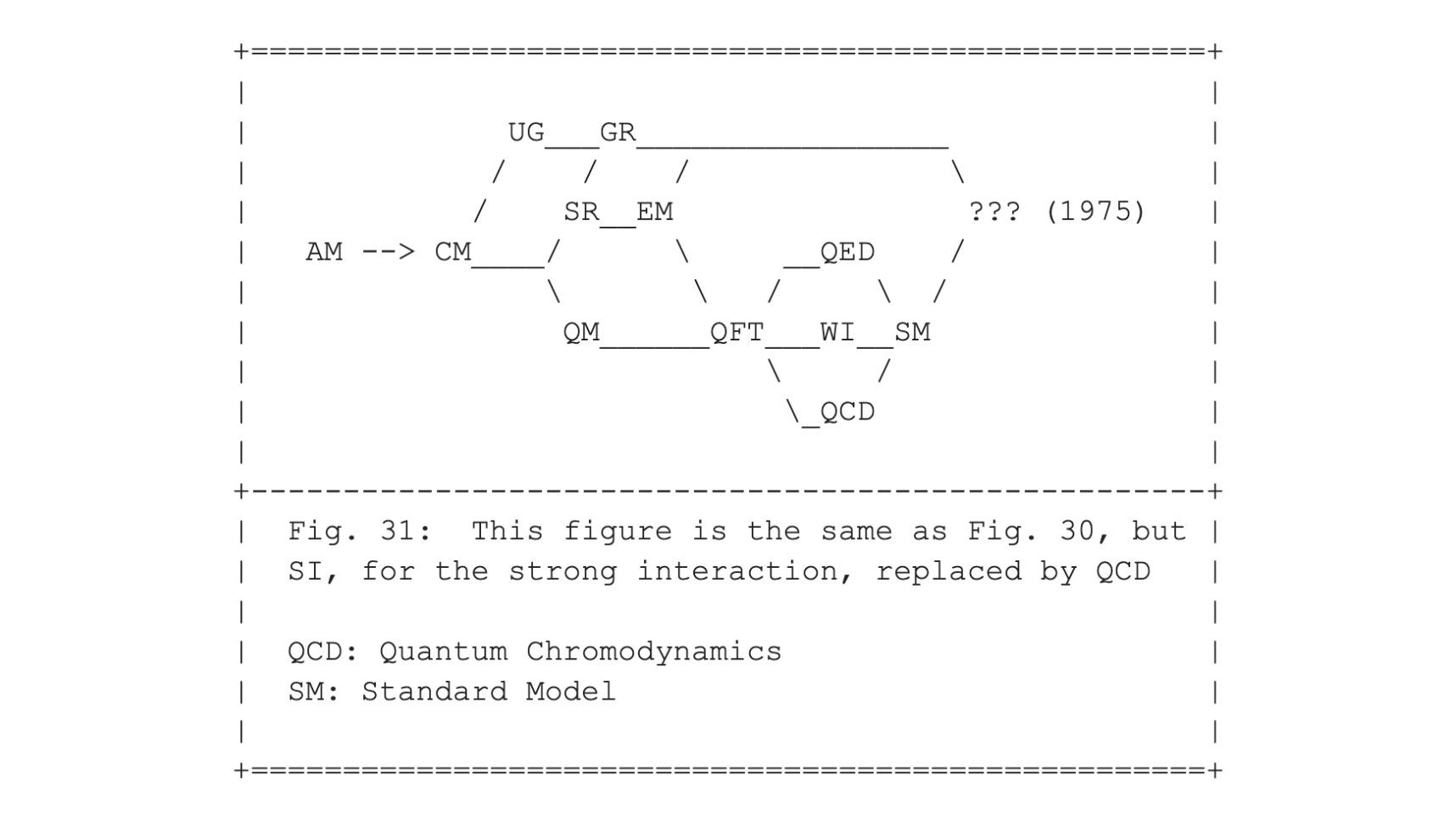
In Fig. 30 I have glossed over a detail that is not important for the current level of exposition. For completeness, I could have replaced SI, for the strong interactions, with QCD, quantum chromodynamics as the field theoretical name for SI. This would be following the same convention in which I replaced EM, for classical electromagnetism, with QED, for its field theoretical counterpart. The result is Fig. 31.
However, to be fully consistent I should also replace WI, for the weak interactions, with its field theoretical counterpart. The problem here is that while QCD corresponds to SI, there is no single QFT that corresponds to WI. Rather, the standard model is formed by a unification of QCD with another theory, modeling the electroweak interactions, EWI, that itself is a unification into one QFT, of EM and WI, the forces of electromagnetism and the weak interactions. I have depicted that situation in Fig. 32, for completeness, but in subsequent figures I will simplify things back to the style of Fig. 31.

Mapping the structure of atoms
Having sketched the theoretical background for the opening of act 3 of physics, followed by presenting a single picture, Fig. 32, it is time to ask "what does this buy me?" The answer is: for the first time in human history we not only know *that* matter around us consists of atoms, we also have arrived at a quantitatively accurate detailed picture of *what* is hiding inside atoms.
As often is the case, a terribly boring way of teaching what humanity has learned so far would be to provide a laundry list of the contents of atoms. This list would then have to be learned by heart by bored students at some time in their schooldays. Instead, let's take a quick walk through history, in order to see how this list was designed in steps, based on new discoveries at each step.
We can start our journey by traveling back in time to the beginning of the previous century. In 1904 the British physicist J.J. Thomson, the discoverer of the electron, proposed a model for the contents of the atom, while wondering what to do with his electrons. It was called the "plum pudding model" of the atom in the popular press (Google tells me that plum pudding is an English dessert similar to a blueberry muffin). In that model the negatively charged electrons were embedded in an amorphous distribution of positive charge, surrounding the electrons like raisins in a plum pudding (or blueberries in a muffin).
Then, in 1911, Ernest Rutherford introduced a model that looked more like the solar system: it had a heavy nucleus in the center, with electrons orbiting around it. The motivation was the fact that electrons, when aimed with high speed at atoms, would occasionally scatter or even recoil at large angles from their original direction of motion, suggesting the presence of small heavy objects in the center of atoms.
Soon afterwards, in 1913, Niels Bohr proposed a model that featured some quantization aspects, in contrast to the previous two models that were purely classical. He posited that electrons circle the atomic nucleus, as in Rutherford's model, but only on specific orbits, like standing waves in a string, thereby introducing a discrete element in the model. Several other physicists proposed variations on this idea, in what later would be called the "old quantum theory", using "semi-quantum" approximations before 1925.
All of these models became obsolete in 1925 in one stroke, or more accurately, in two parallel strokes. That year saw the advent of two initially competing models, Heisenberg's matrix mechanics and Schrödinger's wave mechanics, that were quickly recognized as being equivalent, as we saw in entry #010.
Immediately during and after 1925 the nature of the "electron cloud", filling the atom around the nucleus, was elucidated in detail. It took much longer to determine the nature of the nucleus itself. In 1932 neutrons were discovered, and it was realized that an atomic nucleus is built up of a tightly packed mix of positively charged protons and electrically neutral neutrons, hence the name. Using the term tightly here is not an exaggeration: the size of a nucleus inside an atom can be compared to that of a flea inside a cathedral, spanning roughly one hundred thousandth of the atom.
Soon afterwards, two new forces were discovered, both playing important roles inside atomic nuclei, simply called weak and strong interactions, respectively, in their order of discoveries, as we saw in entry #011. Their bland names indicated the surprise at their discovery and the initial uncertainty as to what they were. The uncertainty would last till 1970, and it was only when the standard model was completed that their roles in atomic nuclei were fully elucidated.
In short, and very much oversimplifying, since 1975 we know that protons and neutrons are each "blobs" of a mix of quarks and gluons. Here quarks are components of protons and neutrons. Quarks are much lighter than protons and neutrons, and gluons are massless: like photons, quanta of the electromagnetic field, gluons can be viewed as quanta of the strong interaction. Most of the mass of protons and neutrons is formed by the energy of relativistic motions of the quarks and gluons, confined inside the protons and neutrons. Its composition resembles a modern version of plum pudding or blueberry muffins, used 70 years earlier by Thomson, but on a scale one hundred thousand times smaller, and with inner turmoil moving close to the speed of light.
Not yet mapping the structure of the cosmos
Having sung the praises of the standard model, let me hasten to mention that act 3, like act 2, is still part of a kind of "middle ages" of physics, carrying in it the seeds of (a) very different period(s) to come. At the danger of pushing the analogy too far, perhaps act 3 can be seen as a renaissance, literally a rebirth, following the middle ages of act 2. As we saw above, 1975 brought a new stability in our understanding of the structure of atoms, from a-tomos, non-divisible and otherwise nondescript things, to a neat inventory of its components. Or with a longer view back, a rebirth of the prescientific model of atoms in four or five forms, in Greece, India, and China.
Whatever future theories will propose for the nature of material reality, the picture of atomic structure drawn using the standard model is here to stay. Any future theory that may replace quantum field theory as a more accurate description of matter of smaller and smaller scales, whatever its structure may be, has to agree with the same experiments that the standard model had to agree with -- just as general relativity had to agree with Newtonian gravity in the limit of weak forces and low speeds.
That said, physicists are certain that the standard model is only a way station on route to a much more filled-out future theory of material reality. For one thing, while doing an amazing job explaining the state of affairs inside the microcosmos of the atom, it utterly fails to give an equally rosy picture for the macrocosmos of the Universe.
In a nutshell: we astrophysicists don't know what we're talking about. More precisely, given that our task is to study the Universe, it is a sobering thought that we only know the nature of 1/20th of the inventory of the Universe. Of the remaining 95%, we have no idea what it is -- or equivalently, we have too many ideas, none of which we can be sure of with any measure.
Ordinary matter, made out of atoms, makes up only 5% of the content of the Universe. Another 25% of the matter in the Universe is invisible. It is there, and can be detected by its gravitational pull on visible matter, but we simply don't know what it is made of. It could be yet unknown types of elementary particles, it could be some type of black holes, it could be many other things sprinkled through the virtual universe of imagination that astrophysicists entertain.
What is even worse: we have no idea what the remaining more than 2/3 of the mass of the universe is made of. This "mass", being equivalent to energy, can be made of something more resembling energy, perhaps the energy inherent in the structure of the vacuum of our Universe. With that in mind, the 25% that is missing is called "dark matter", in that it does not seem to interact with electromagnetic radiation, and the rest that is missing, the bulk of the content of the cosmos, is called "dark energy", since it is not condensed in or around clusters of galaxies, the way "dark matter" is. The fact that it is spread out almost evenly hints at it moving at very high speed, meaning that its energy of motion is far higher that the equivalent rest mass it has, if any.
Apart from its inability to explain the contents of the Universe, there is much more that is still "missing" in the standard model. Shifting our view from space to time, to the start of our Universe in the Big Bang, the standard model has nothing to say about the Planck time, as it is called, a time at which the energy density of the Universe was so large that the force of gravity was as strong as that of the forces displayed in the standard model. The Planck time is very short: 5x10^-44 seconds or in the ballpark of a quadrillionth of a quadrillionth of a quadrillionth of a second.
To sum up: we astrophysicists don't know what we are talking about and we don't know where we're coming from. Such an exciting time to be an astrophysicist, given that we do have reason to believe that we are getting closer to the answers to both questions! "Any day now" would be an exaggeration, but "possibly in a decade (or two)" may not be unreasonable as a guess.
Anatomy of the standard model
Above I used the metaphor of mining the history of physics, in search of clues for theory formation, to apply those to our burgeoning science of mind. I will now switch to another metaphor: let's make an attempt to uncover the anatomy of the standard model. Which historical theories "fit into" later more expanded theories, how do they fit, and what does "fit" mean?
Let us return to Fig. 31, including QCD, quantum chromodynamics, in a slightly expanded version, which is given in Fig. 33. Here classical electricity and magnetism are added as E and M before they were unified into electromagnetism by Maxwell. To be precise, in entry #011, Fig. 29 showed the genealogy of EM, with EM taking the place where Maxwell had put it, whereas the current place of EM, after Einstein's discovery of relativity, can be spotted in Figs. 28, 31, and 33 in this entry.
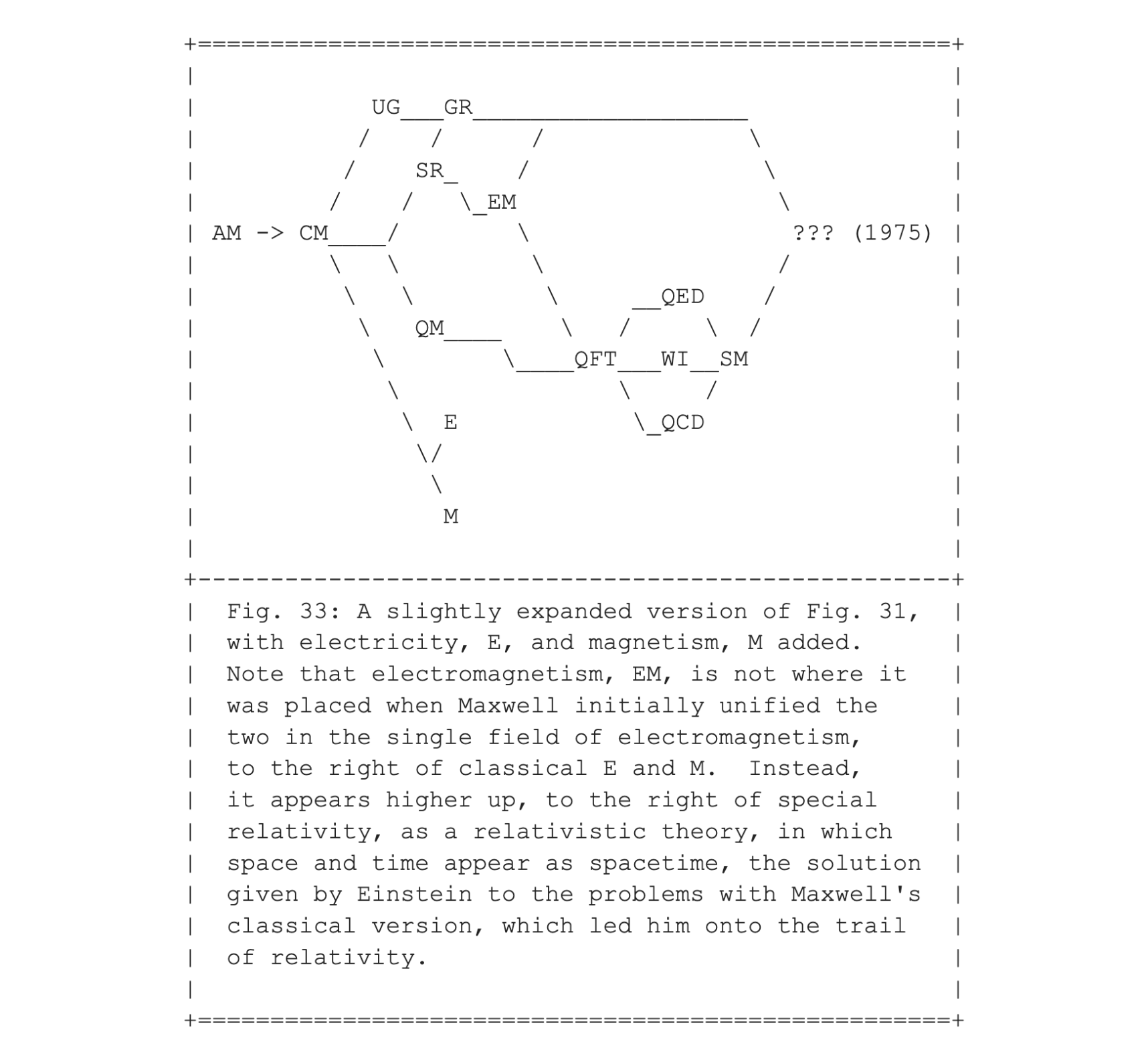
Now that we are up-to-date as to our best theories of the nature of matter, in terms of the smallest constituents we know and the interactions between them, let us step back and make some anatomical snapshots as to which parts of the theory "fit into" other parts. "Fitting in" is used here in the sense that Newton's theories "fit into" the wider theory of Einstein's general relativity by giving the same results in the limit of weak gravitational theory. Another way to express this is to say that Einstein's theory is "bigger" or "more accurate" than Newton's theory.
The simplest form of "fitting into" is a straightforward nesting of a series of theories, like that of Russian dolls. From Fig. 33, we can read off an example, in the way that classical mechanics, CM fits into special relativity, SR, which in turn fits into general relativity, GR. Using the symbol "<" for "fitting into", we have CM < SR < GR. Another example is CM < QM < QFT, with QM for quantum mechanics, and QFT for quantum field theory.
The latter two are examples of what mathematicians call a total ordering. More frequently, we are confronted with what is called a partial ordering. Fig. 33 shows the following four fitting relationships: CM < SR, CM < QM, CM < QFT, but there is no fitting relationship between the two middle players, SR and QM.
Each of the pictures we have used up to now, starting in the first Picture book entry, #008, shows fitting relationships, deepening when we move further to the right. One potentially confusing aspect of these figures is that moving to the right can also indicate "with examples of" instead of "fits into". Whenever moving to the right branches into more than one path, we are dealing with examples. For QFT, quantum field theories, three examples are given in Fig. 33, that of quantum electrodynamics, QED, and WI and QCD for the weak and strong interactions.
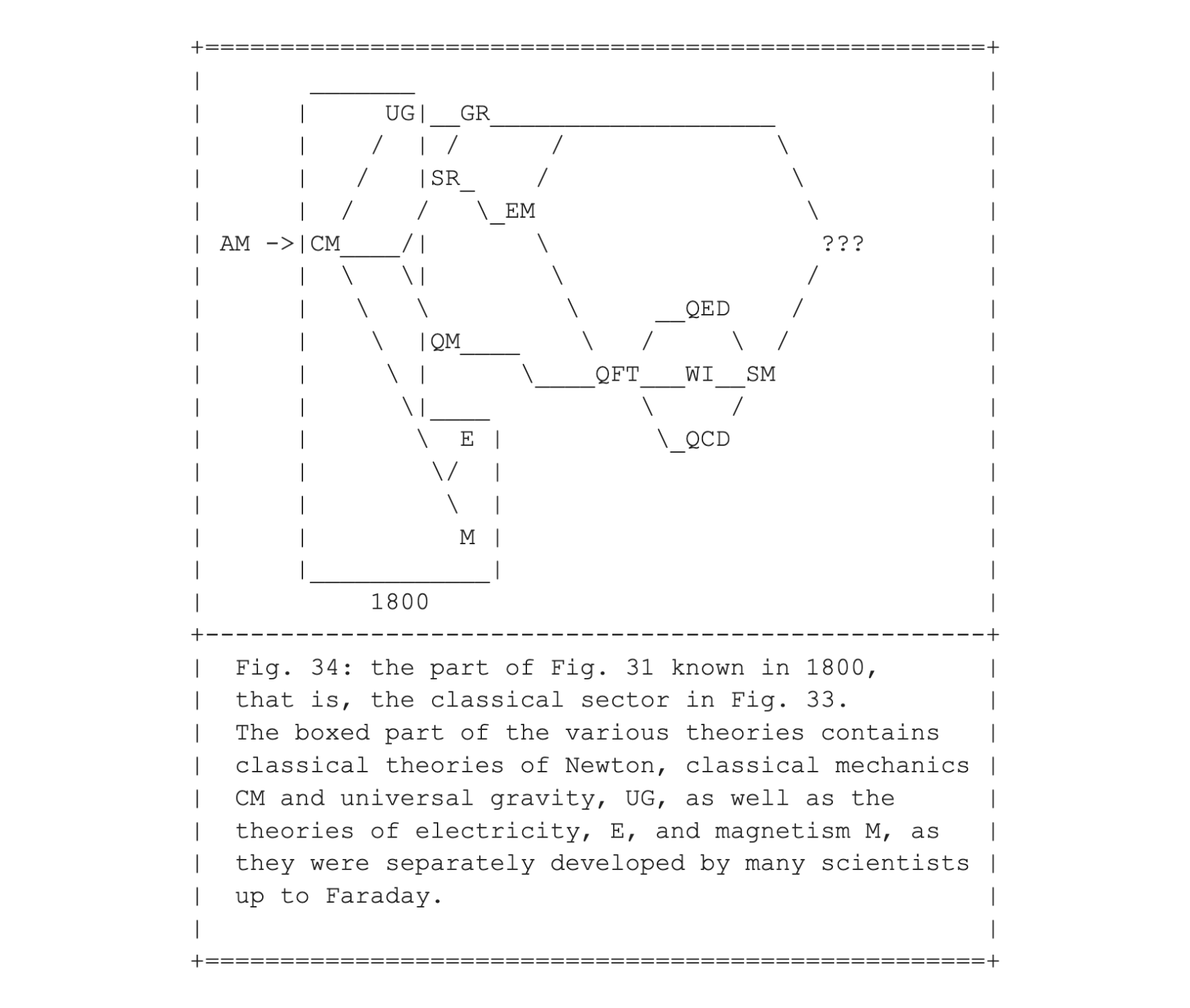
Fig. 34 shows the first anatomical picture, in the form of what was known a bit more than a century after Newton. A detailed study of electricity, E, and magnetism, M, had begun and the various theories of increasing accuracy of detail all neatly fit into the classical paradigm established by Newton.

Fig. 35 shows the anatomy of physics theories a bit more than a century later. Newton's classical theories are seen to fit into the extensions provided by Einstein, including Einstein's further extension of Maxwell's theory of electromagnetism.

Fig. 36 shows the state of anatomy in 1925, after the arrival of the shock of the discovery of quantum mechanics. It seemed that the parts of the body of physics no longer fit together! Following road signs pointing from classical mechanics to wider views would lead you to different hills, each with a sign pointing to the other hill reading "you can't get there from here".

Fig. 37 shows the next picture Rip van Winkle would have seen, had he slept for 50 years instead of 20. All would be well after the quantum field theory revolution had taken place. There was not even a need to change the hill signs: the two hills turned out to be different sides of the same hill.
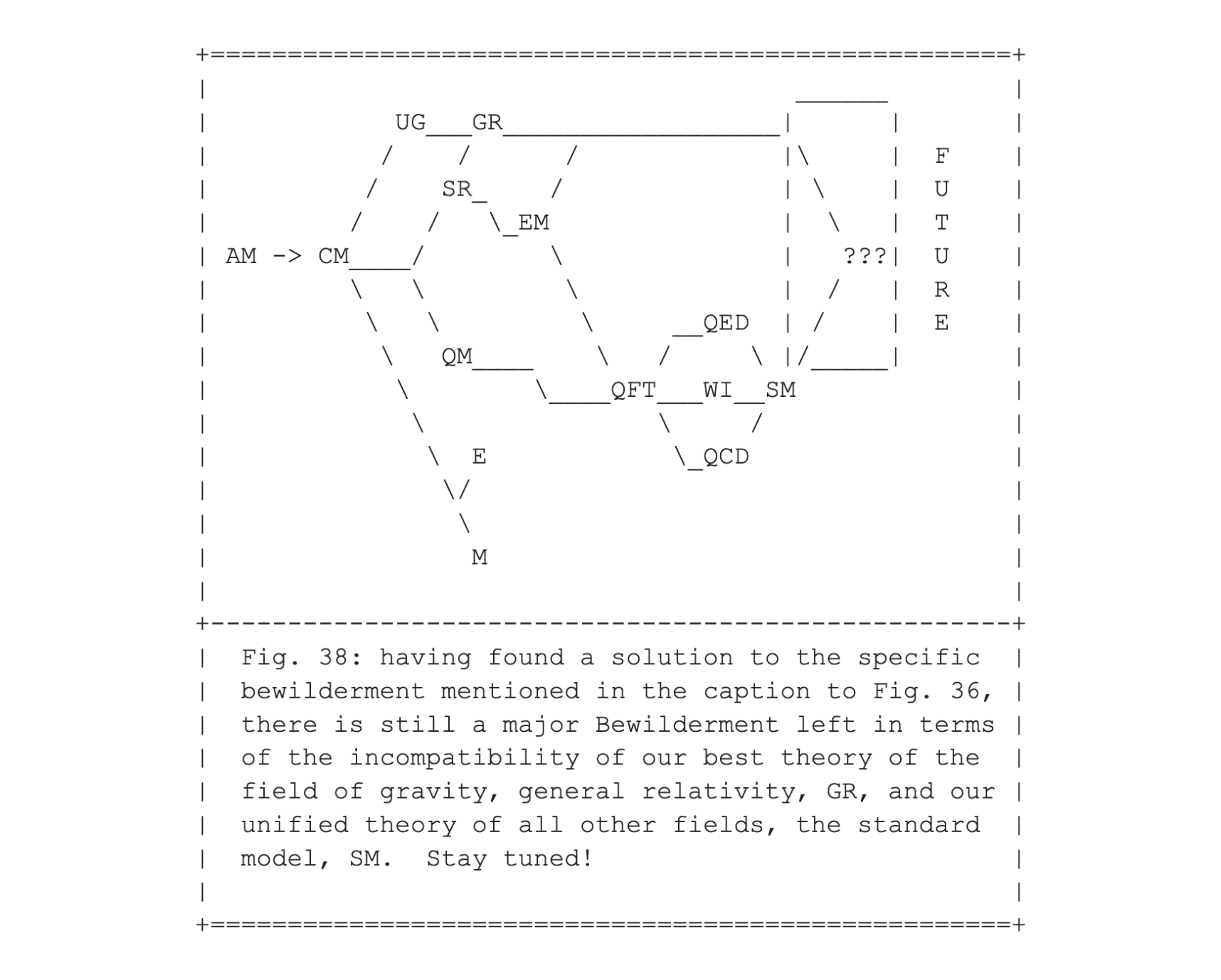
Fig. 38 points to a future time when the spacetime based gravitational field and all other material fields will have been unified in an as yet unknown way. We currently have no idea what it will look like, nor do we know how long Rip van Winkle would need to sleep, were he to start his next nap today.
Wrapping up
This anatomy lesson, while lacking the elegance of Rembrandt's painting with that name, I am planning to use in subsequent entries as comparison material. Specifically, I will introduce and explore hypotheses concerning relationships between matter, experience and appearance, beyond what I described initially in entries #003, #004 and #005.
These hypotheses I will develop using the working hypotheses, introduced in entries #003 and #008:
WH 1: there are primitive elements underlying experience
WH 2: appearances are primitives for any form of experience
WH 3: the shifts in perspectives between viewing objects as matter, experience, or appearance, might have analogies in the shifts of perspectives between subsequent theories in physics.
In particular, we will encounter situations that might be analogous to Fig. 34, where the boxed part could correspond to what Husserl called the natural attitude, as we saw in entry #004. Fig. 35 could offer a simple model for what might happen when we zoom in on specific aspects of the natural attitude, say E and M in Fig. 35. Such inspection can hold clues as to the existence of a whole new sector beyond the natural attitude, necessary to show how elements like E and M can be unified into EM in ways for which there is no room in the boxed part of Fig. 34.
I will use Fig. 36 as inspiration for a comparison between the way Galileo introduced mathematics as a kind of "transcendental" probing of material processes and Husserl introduced his epoché to probe what he called the nature of the "transcendental" subject. In that figure, the boxed part shows candidates for two different extensions of the same initial attitude that at first sight seem blatantly incompatible, only to be unified later through a wider perspective.
The boxed part in Fig. 37 can serve as inspiration, if nothing else, for persistence in dealing with unexpected discoveries that lead to dead ends for many decades. Such discoveries might suddenly offer equally unexpected and truly marvellous solutions to problems one didn't yet know were lying in wait.
To wit: quantum mechanics upset the apple cart of classical mechanics. But fifty years later, in just a few years, quantum field theories provided a coherent quantitatively accurate picture for material reality -- down to quarks and gluons, now seen as internal parts of protons and neutrons, which themselves are parts of the atomic nucleus, which in turn is the central part of each atom. What a marvelous solution, so far beyond anything that a mechanical model could have provided!
Finally, Fig. 38 reminds us that a final near-miraculous solution to one persistent problem can highlight the next, even more persistent problem, and in doing so, can provide new clues for that next-in-line problem.
Note that in all this I make no claim, in fact not even a hypothesis, that any of the figures mentioned above have any direct relationship with the various possible analogies I just mentioned. Rather, what inspires me is the fact that in natural science very often mathematical models developed for one application have found quite different applications in seemingly totally unrelated areas. The most conservative guess for what will happen in a science of mind would be that such a pattern of discoveries will continue, and at least we should keep an open eye for such a possibility.
– Piet Hut