The State of Physics in 1925
FEST log
Entry #010
June 13, 2024
The opening of physics, act 2: a quantum world
At the end of the previous entry, #009, I described how the curtain dropped on physics, act 1: a classical world. The second act of physics started in 1925 with the discovery of "quantum mechanics", a radical break from "classical mechanics", which was the name of the game of physics from Newton, via Maxwell, and through Einstein's special relativity and general relativity.
Of course, physicists before 1925 didn't know they were doing research in classical physics, just as ancient Greek and Roman writers didn't know at the time that they were writing "classic" literature. Nor did Thomas Aquinas know that he was a "Medieval" writer.
Here the analogy breaks down, though. From the beginning of the era of quantum mechanics, it was clear that there were serious problems, which seemed to point to solutions that had to be more radical, whatever their nature was going to be. In that sense, physicists knew that they had entered a kind of "Middle Ages" which were likely to end, sooner or later, when deeper insight would be obtained.
In this and the next two entries I will sketch the state of the art of fundamental physics in 1925, 1950 and 1975, respectively. At each of those last two moments in time a major breakthrough was made in clearing up some of the fog that had descended in 1925. But, with a spoiler alert: no comparable breakthrough has happened in 2000, nor is it obvious that it may happen in 2025 or anytime soon thereafter.
So it seems that we'll remain in the "Middle Ages" more than a century after the end of the "Classical Period". Even so, there are plenty of hopeful signs that fundamentally new insights will be reached, either through theoretical or experimental breakthroughs, or even better, through both.
A happy family and an unexpected new arrival
To prepare the stage for the events that shook physics in 1925, I am presenting here again Fig. 12 from entry #009, the "family portrait" of all the interlocking parts of the four-dimensional machinery of physics in 1915.
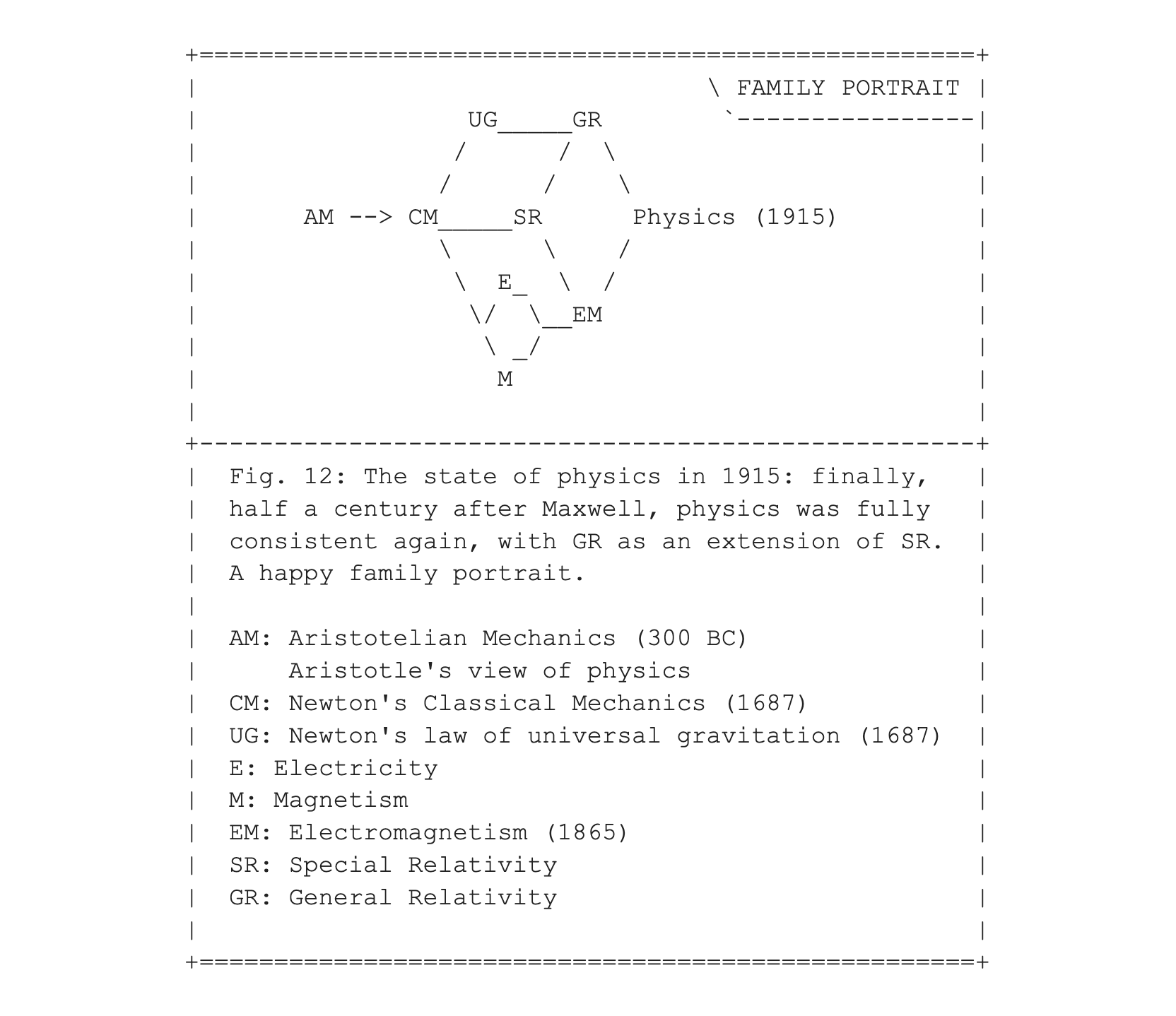
In this figure, you can see that Maxwell's theory of electromagnetism (EM) was not only a unification of the various effects already known for the interplay between electricity (E) and magnetism (M). Unbeknownst to Maxwell, Newtonian classical mechanics (CM) was not able to explain the observations of waves in the electromagnetic field until CM was replaced by the theory of special relativity (SR). Without the combined help of SR and EM, there would have been no way to unify the theories of E and M, as depicted in Fig. 18.
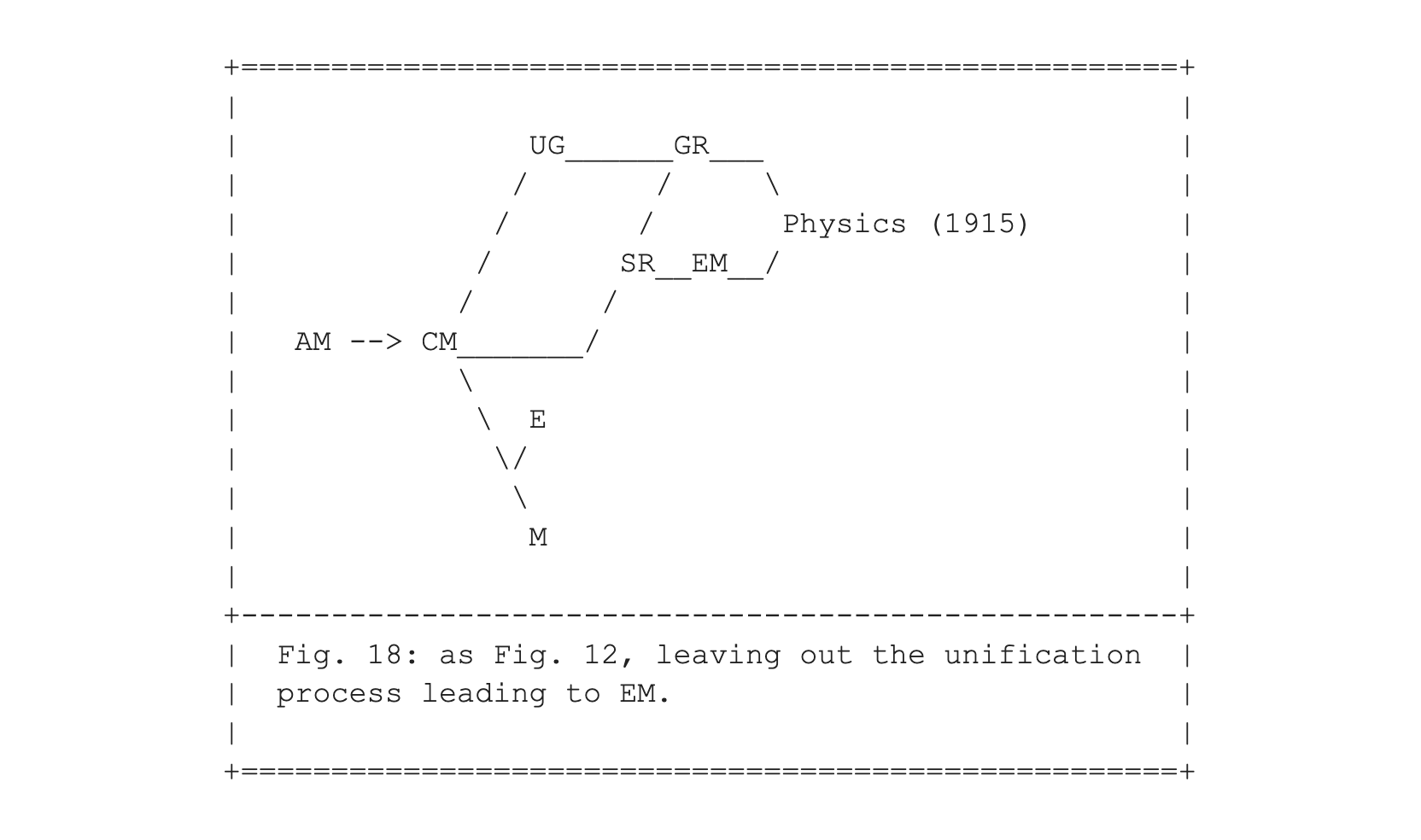
I have presented Fig. 18 here as a first step toward introducing the new arrival "out of nowhere" who joined the happy family of Fig. 12. In Fig. 19 we fast forward to 1925, where quantum mechanics (QM) is introduced.
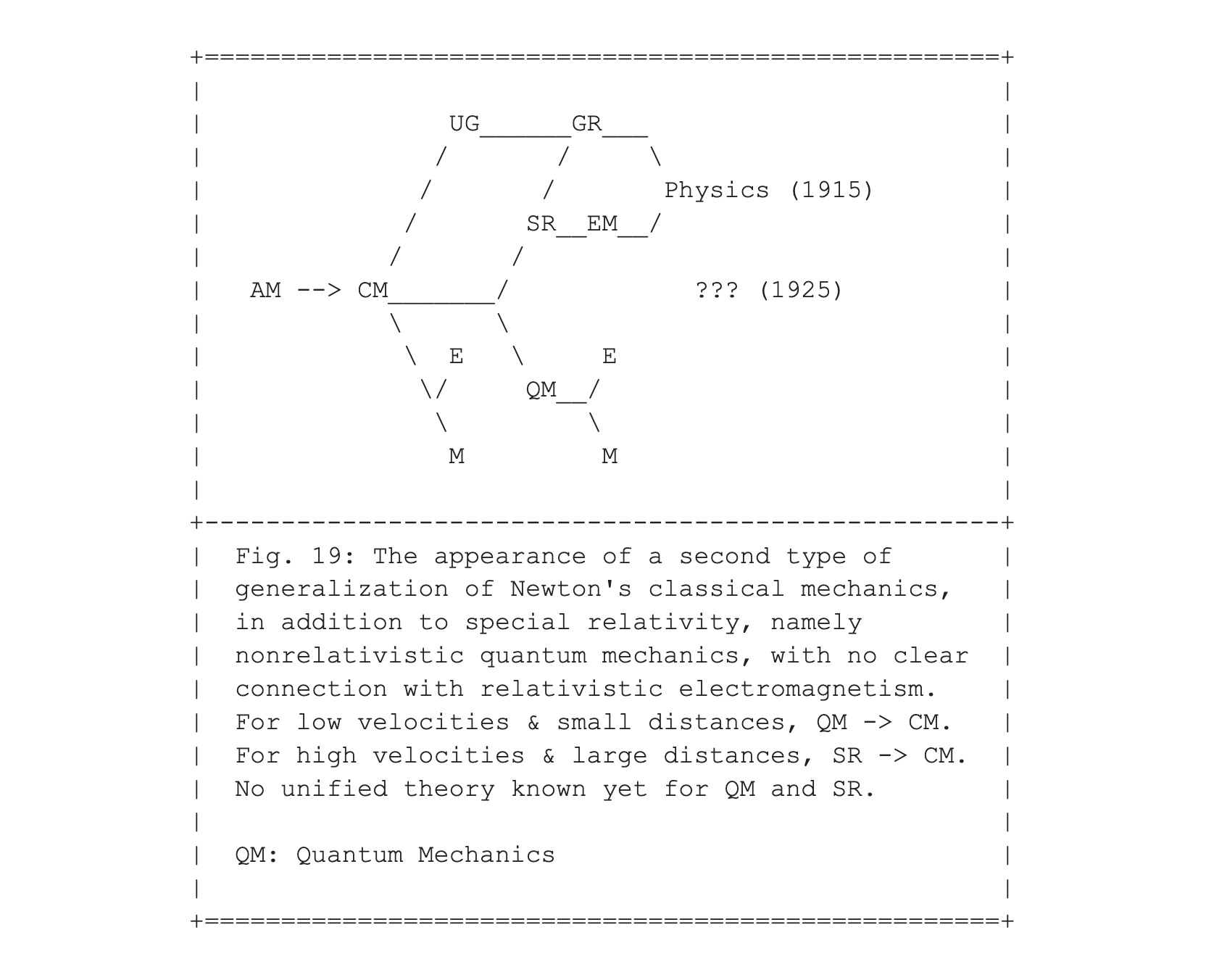
Quantum mechanics . . .
Where Newton had built a firm stage made of absolute space and time to let objects dance on, under the influence of gravity, Einstein had created a flexible stage. It was a stage that itself partook in the dance, more like a kind of trampoline, made of a dynamic spacetime, that could stretch and twist and turn. But a decade later, an even much more revolutionary theory was put forward. Quantum mechanics corresponded to a move to an altogether different theory -- through the looking glass into a world more like that of a fairy tale.
From a dance on a fixed stage with fixed rules, to a stage that was dancing with its players, but still with fixed rules, to a dreamlike world in which everything is possible -- but with fixed rules for the probability of anything to happen. The mathematical background spaces for quantum mechanics are altogether different from anything classical. The spaces used to calculate probabilities for any type of outcome are no longer given in terms of space and time, but rather in terms of abstract complex high-dimensional Hilbert spaces.
Instead of moving to a different stage, as physics had done twice, in 1905 and 1915, in 1925 physics moved into an altogether different theater building, if not into an altogether different world. This is not the place to present an introduction to quantum mechanics, but there are plenty of introductions available on the internet and in book form, on many different levels.
The bottom line is that from 1925 onwards, physical reality on its most fundamental level had no longer any clear meaning. Sure, twenty years earlier, already with the disappearance of an aether, there was no clear picture of how there could be waves in a field without there being a medium -- electromagnetic waves just seemed to be "waving" in a total vacuum. But at least there was a comfortably objective picture to describe those waves, one that everybody could agree on.
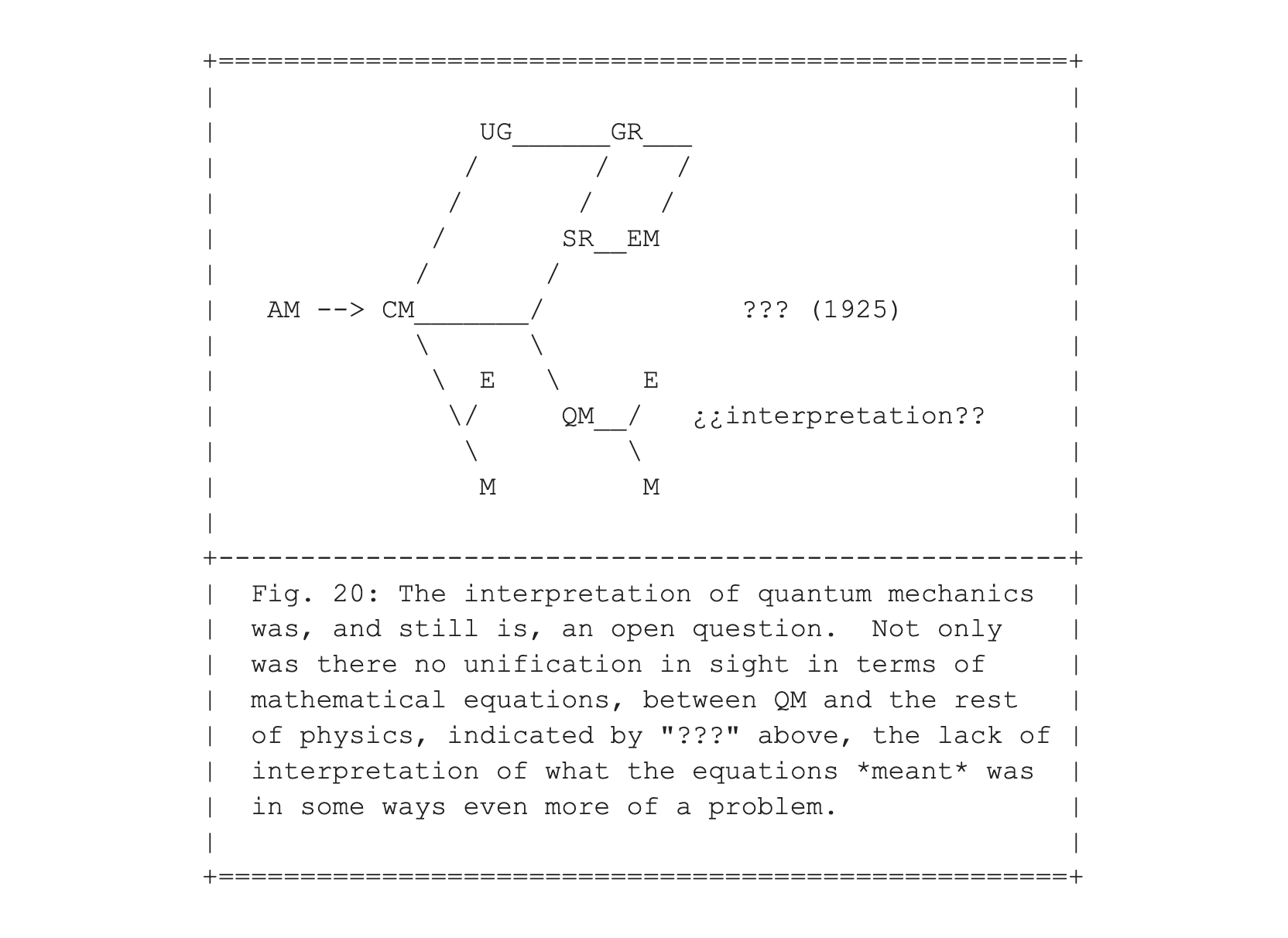
The momentous difference between classical and quantum physics is that it is no longer obvious whether there even is an objective world out there. More precisely, of whether an objective description of the world is something that is not observer dependent. Currently there are numerous different interpretations of quantum mechanics, some of them based on intersubjective agreements of measurements, without requiring, or even allowing, an objective background world.
I am hesitant to even begin selecting some pointers to the literature, among the hundreds of books that have been written on this topic. Fortunately, for the purpose of my narrative in this and the next two entries, I can strongly recommend the book "Waves in an impossible sea" by Matt Strassler which came out just one week after I started this Log. It gives the clearest description I have seen of the roles of fields and waves and many of the seeming paradoxes of quantum field theory (the topic of entry #012), on a surprisingly clear non-technical level.
An unhappy family
In entry #009, Figs. 13 and 15, I presented a comparison between three happy families: the Newtonian classical mechanics view of physics around 1700, the Maxwellian picture, still the best one around in 1900, and the Einsteinian picture arrived at in 1915. They all looked alike.
Following Tolstoy's observations at the start of his novel Anna Karenina, “All happy families are alike; each unhappy family is unhappy in its own way”, the unhappy family, shown in Fig. 21, definitely looks very different from anything seen before.
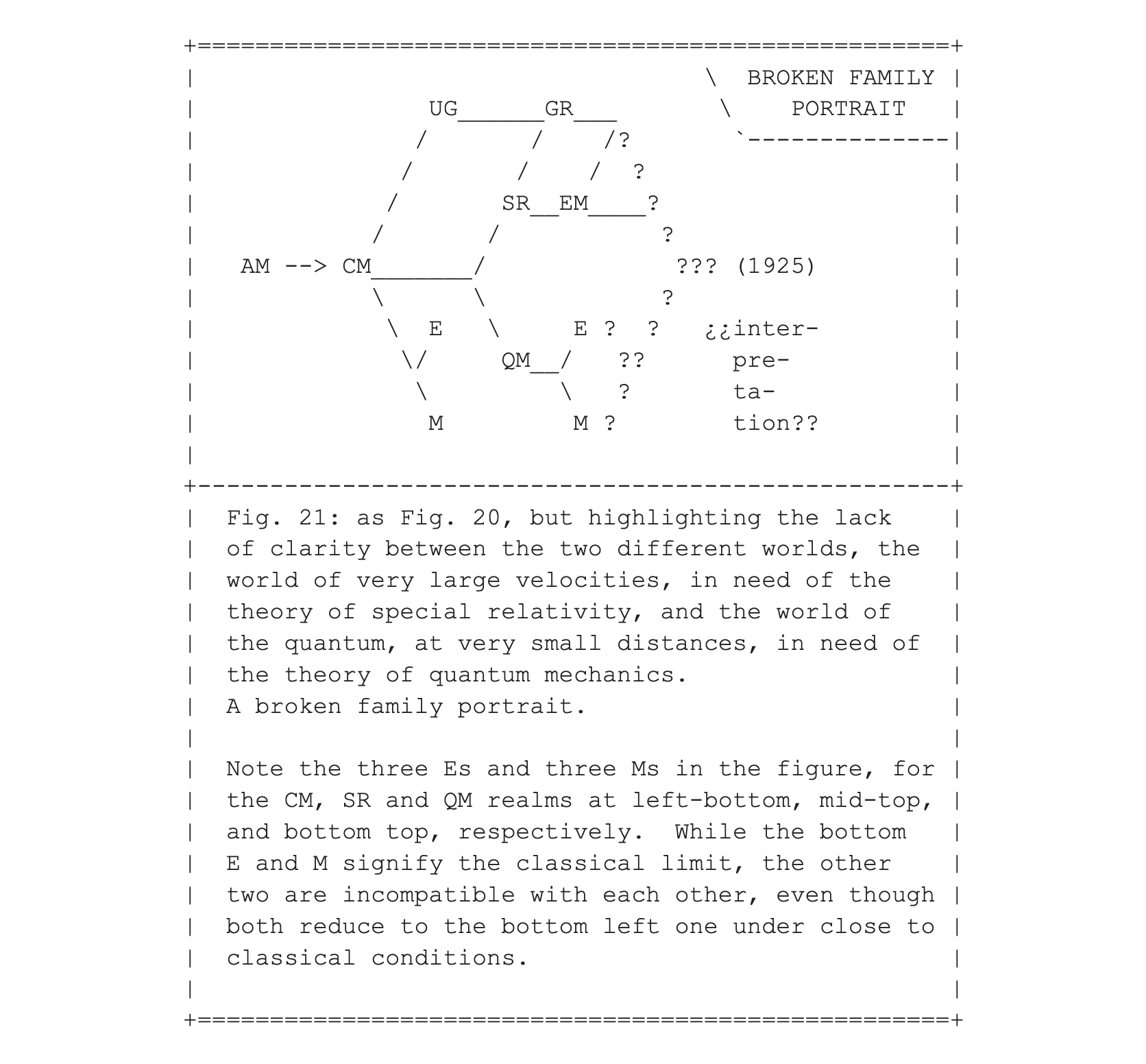
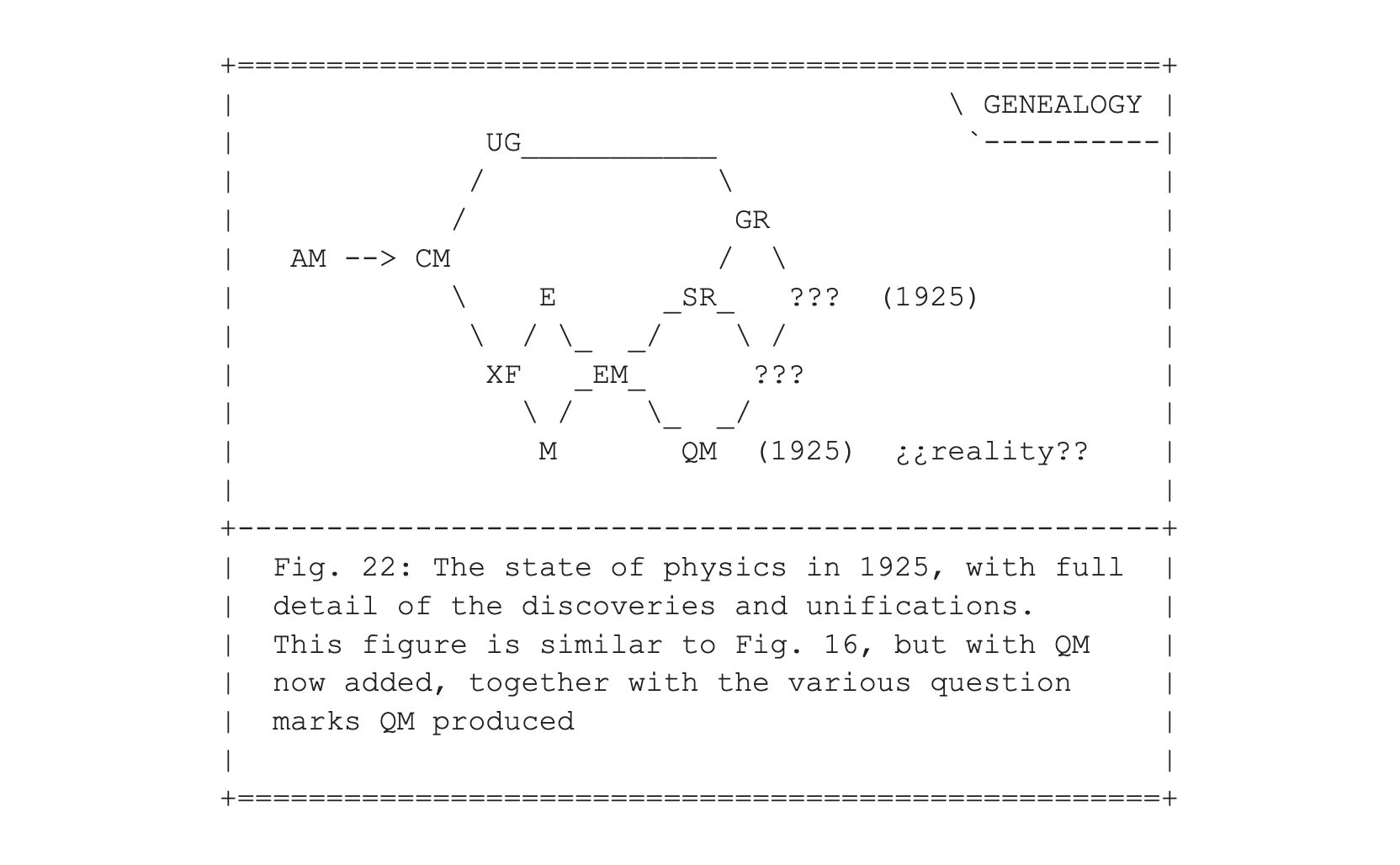
To make another comparison with entry #009, the genealogy figures, Figs. 16 and 17, now get enriched with quantum mechanics, to produce Figs. 22 and 23.

Early warning signals
The way I presented my very short summary of the advent of quantum mechanics has left out many important details. Yes, the full paradoxical nature of quantum mechanics was totally unexpected. Even so, during the 25 years running up to 1925 it already became increasingly clear that *something* was going on that was likely to shake the foundations of physics.
It started in 1900, when Max Planck coined the word "quantum". He did so to give a name to an observation that he had made. He noticed that the behavior of some forms of radiation could be explained by an ad hoc postulate that this radiation could only be emitted in the form of discrete energy packages, which he called quanta. He realized that, using this strange and unnatural postulate, things fell into place that otherwise didn’t make any sense. But at first he had no idea how revolutionary the consequences of that first step would become.
Before 1925 at least a dozen scientists made significant contributions to the framework of what would become full fledged quantum mechanics in 1925, including Einstein, Bohr and de Broglie. And when finally quantum mechanics got off the ground, there were another dozen scientists who made significant contributions, right in the first two or three years. Most prominent were Heisenberg and Schrödinger, each of which found a rather different approach to what would turn out to be the same underlying theory. But many others, like Born, Dirac and Pauli, made essential contributions as well.
A shift towards collaborative efforts
In that sense, the discovery of quantum mechanics as a theory was rather unlike the discoveries by Newton, Maxwell and Einstein. In each of those three cases, too, several other physicists had made very important breakthroughs that provided essential building blocks for the final discoveries. But still, there was this magical moment when one person managed to put everything together, showing that everything "clicked", as in finding the places for the last pieces of a puzzle.
Quantum mechanics was different, and indeed during the next hundred years after the discovery of quantum mechanics, there never was a particular insight of a single person that started a whole new approach to theory building in fundamental physics.
Finally one more aspect that I have left out: I have not mentioned in my history of physics the very important role of thermodynamics and statistical mechanics, developed in the nineteenth century, which gave physicists experience in working with calculations involving probabilities. Such a discussion would deserve at least one more entry in this log.
What we have seen so far
Looking back to the beginning of this FEST Log, three months ago, the first five entries, #001 through #005, have centered on a very brief initial exploration of the nature of experience. Since the FEST program aims at establishing a science of mind, experience is an obvious place to start. I suggested some possible directions for setting up an initial and very simple theory of experience. In addition, I also provided some sketches for experimentation.
My aim was to show early on how to get the "ratchet of science" started: developing new experiments to test the latest theory, followed by developing new theories more in line with the results from the latest experiments, and so on. I described the "ratchet" in entries #001, #003, and #006. And in order to make initial contact with recent literature, I found it helpful to mention two philosophers, Husserl in entry #004, and Nishida in entry #005, both of whom did their work in the early twentieth century.
However, already in entry #002, I argued that it makes sense to turn to the treasure troves of prescientific studies of the mind, that have been preserved in oral and written form, in various contemplative traditions in many cultures. Following the example of astronomy, the foundations of which were laid by a millennium of Babylonian observations, I named a number of still living traditions that might give us inspiration as well as specific sets of observations.
The biggest problem in receiving inspiration for setting up theories and interpreting observations from ancient traditions is sectarianism. Imagine that scientists in different fields of physics would not talk to each other, and only or mostly discuss their specific field among themselves. That would be a similar situation as what prescientific engineers were limited to, keeping their knowledge within their own circles.
What we might learn from physics for a science of mind
Following our short initial exploration of the nature of experience, from entry #006 onward we started to analyze the structure of theories of physics, in order to have at least one example of an evolving set of theories, all empirically based. Hopefully, this can give us some inspiration for setting up a tentative theory structure, based on observations gleaned from contemplative traditions.
To make this a bit more formal, starting with entry #008, I introduced a new working hypothesis:
WH 3: the shifts in perspectives between viewing objects as matter, experience, or appearance, might have analogies in the shifts of perspectives between subsequent theories in physics.
One reason I think this might work to some extent, is that all contemplative traditions I am familiar with have a nested set of instructions for view and practice, from simple and practical for lay persons, to more and more refined forms within monasteries or other communities focused entirely or mostly on contemplation. If we translate view into theory, and practice into experiment and observation, the parallels with physics, as we have seen in our set of diagrams so far, is striking.
In order to go to the Moon, classical mechanics is good enough. But in order to find our way in a city, when we use GPS, we are using software that is based on general relativity, since the accuracy required goes well beyond that of Newton's theory of universal gravity. To study the outlines of a living cell, and the ways cells are packed together, again classical mechanics can do a good job. But to model the details of small-scale processes within cells, sooner or later we have to take quantum mechanics into account. In fact, all of chemistry is based on quantum mechanics on the atomic level.
The similarity of nested structures of theories in physics and in contemplation, which became more and more clear to me, was my main motivation for delving into the nested structure of theories of physics, as they evolved over time. Before long we will start making specific comparisons between some contemplative traditions and their nested views and the structure of their physics counterparts. Let us see how far we can get, in making at least some initial progress in setting up a candidate for a foundation of theory building for a science of mind.
With that goal, we will visit the history of physics of the last century, from 1925 till now, in the next two entries. Following that, we will take a break and sum up what we have learned, thereby concluding Part 1 of this FEST log. My aim is to bundle together a dozen or so entries in each Part, together with a postscript summarizing the structure and contents of that particular Part.
– Piet Hut