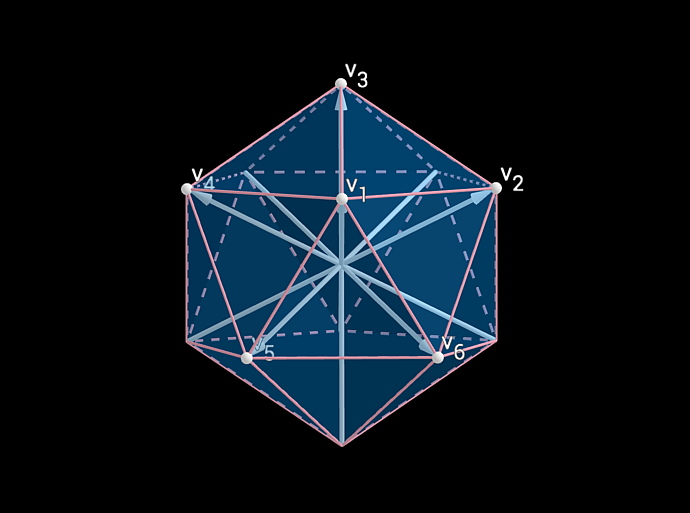
A New Path to Equal-Angle Lines
Equiangular lines are an elemental part of geometry. . . . Mathematicians want to know just how big those sets can get as you move past the 3-D space of our everyday experience and into higher dimensions.
Last spring a team of mathematicians found the maximum number of equiangular lines possible in any dimension, given certain conditions. They proved that that number is much smaller than previous best estimates. Benny Sudakov, former Member in the School of Mathematics, professor of mathematics at the Swiss Federal Institute of Technology Zurich, and one of the lead authors, credits the breakthrough to the wide range of mathematical techniques he and his coauthors were able to apply to the problem.
“It’s like when you’re cooking something, we suddenly found we had the right ingredients,” said Sudakov.
Read more at Quanta.


